LTO (Linear Tape-Open) tape
LTO (Linear Tape-Open) tape is an open-format tape storage technology created by Hewlett-Packard (HP), International Business Machines (IBM) and Seagate Technology. The term open format means users have access to multiple sources of storage media products that are compatible.
The high-capacity, single-reel implementation of LTO technology is known as the LTO Ultrium format, or simply LTO Ultrium.
HP, IBM and Seagate commenced work on the joint tape initiative in 1997, and they delivered the LTO tape format specifications, technology roadmap and license availability the following year.
Seagate's tape business became Seagate Removable Storage Solutions in 2000, and the spinoff business took the name Certance in 2003. Quantum purchased Certance in 2005. HP -- now Hewlett Packard Enterprise (HPE) -- IBM and Quantum -- members of the LTO Consortium -- continue to enhance LTO Ultrium and promote the LTO tape format.
The LTO Program requires that vendors licensing the technology pass annual third-party compliance verification tests. LTO Ultrium format-compliant products typically carry verification trademarks on tape drives and data cartridges.
Advancements in LTO technology involve the materials from which the magnetic tape is manufactured, the digital encoding and compression methods used, the physical speed with which the tape moves through the drive, the length of the tape in each LTO cartridge, and the physical density of the data bits on the tape. Additional capabilities added with subsequent generations include write-once, read-many (WORM); data encryption; and partitioning to enable a Linear Tape File System (LTFS).
While tape has lost favor to disk and cloud as a storage medium for daily backups, it remains popular for long-term backup and archiving because of its capacity, cost and reliability. As the amount of data continues to grow exponentially, tape is a good option for storing large volumes of data. Industries that create sizable amounts of data each day, such as those in the media, entertainment and sciences sectors, often use tape as a low-cost storage option.
Off-site and offline LTO tape is an option for disaster recovery (DR). If a primary data center breaks down or if a ransomware attack hits, an organization can restore data from a tape backup. While disk-based backups provide quicker recovery, tape has the advantage of being inherently offline, and thus safe from viruses.
Magnetic tape is also an option for large data transfers. Transferring terabytes of data to the cloud, for example, can take much longer over a network than with an LTO tape. In addition, that tape can serve as a backup.
LTO generation roadmap
The LTO Ultrium technology has evolved through several generations since its introduction in 2000, and the LTO Ultrium roadmap provides the goals and objectives for future generations.
A new edition of LTO tape typically comes out every two or three years, doubling the capacity of the prior generation. As of July 2018, LTO-8 is the current edition.
LTO-1: Generation 1 provided a native capacity of up to 100 gigabytes (GB) and a compressed capacity of up to 200 GB, assuming a compression ratio of 2:1. The maximum native data transfer rate was 20 megabytes per second (MBps), and the maximum compressed transfer rate was 40 MBps.
LTO-2: Generation 2 doubled the maximum storage capacity and data transfer rate over the prior LTO-1 generation. LTO-2 provided a maximum native capacity of 200 GB and a maximum compressed capacity of 400 GB. The maximum native data transfer rate was 40 MBps, and the maximum compressed transfer rate was 80 MBps. LTO-2 offered backward read/write capability with LTO-1 tape cartridges. Generation 2 products became available in 2003.
LTO-3: Generation 3 products became available in late 2004 and provided native data storage capacity of up to 400 GB and a compressed capacity of up to 800 GB. The maximum native data transfer rate was 80 MBps, and the maximum compressed transfer rate was 160 MBps.
LTO-3 added WORM capability to ensure data was not overwritten and to help address compliance regulations. Generation 3 offered backward-compatible read/write capability with LTO-2 cartridges and backward read capability with LTO-1 cartridges.
LTO-4: Generation 4 products reached the market in 2007 and provided a native storage capacity of up to 800 GB and a compressed capacity of up to 1.6 terabytes (TB). The maximum native data transfer rate was 120 MBps, and the maximum compressed transfer rate was 240 MBps.
Generation 4 added data encryption using the 256-bit Advanced Encryption Standard with the Galois/Counter Mode algorithm implemented at the LTO drive level, enabling compression before encryption.
LTO-5: Generation 5 products became available in 2010 and offered a maximum native storage capacity of 1.5 TB and a maximum compressed capacity of 3 TB. The native data transfer rate was up to 140 MBps, and the compressed transfer rate was up to 280 MBps.
Generation 5 added partitioning to enhance file control and space management via LTFS. One partition holds the file and another partition is reserved for indexing to tell the LTO drive where a file is stored on the tape.
LTO-6: Generation 6 became available in 2012 and provided a maximum native storage capacity of 2.5 TB and a maximum compressed capacity of 6.25 TB. Generation 6 was the first LTO generation for which the compressed capacity assumed a compression ratio of 2.5:1 through a larger compression history buffer. Generations 1 through 5 assumed a compression ratio of 2:1.
The native data transfer rate for Generation 6 was 160 MBps, and the compressed data rate was up to 400 MBps. LTO-6 supported previously added features such as WORM, hardware-based encryption and partitioning, enabling LTFS. As with prior LTO generations, LTO-6 drives provided backward-compatibility with the ability to read/write LTO-5 cartridges and read LTO-4 cartridges.
LTO-7: Generation 7 became available in 2015 and provided a maximum native storage capacity of 6 TB and a maximum compressed capacity of 15 TB. The native data transfer rate was up to 300 MBps and the maximum compressed rate was 700 MBps. LTO-7 offered partitioning, encryption and the WORM feature.
LTO-8: Generation 8 became available in 2017 with a maximum native storage capacity of 12 TB and a maximum compressed capacity of 30 TB. The native data transfer rate is up to 360 MBps and the maximum compressed rate is 750 MBps. LTO-8 offers partitioning, encryption and WORM.

LTO-8 tape drives are backward-compatible to one generation, so they can read and write to LTO-7 tapes, which marks a change from previous versions that could read back two generations. In LTO-8, tunnel magnetoresistance (TMR) technology and barium ferrite limit the backward reading functionality. TMR, a switch from giant magnetoresistance, increases density in the tape head, and barium ferrite improves capacity.
A new feature, the LTO-7 initialized LTO-8 Type M cartridge, can write 9 TB of uncompressed capacity and 22.5 TB of compressed capacity on a new LTO-7 cartridge, more than the standard 6 TB and 15 TB, respectively. Only an LTO-8 drive can read that initialized tape cartridge.
According to a report from HPE, IBM and Quantum, approximately 108,000 petabytes (PB) of compressed tape capacity shipped in 2017, an increase of 12.9% over 2016 and equal to about 25 billion DVDs worth of data.
Important features
Compression enables an organization to store more data than the native capacity allows. LTO generations 1 through 5 featured a compression ratio of 2:1. Starting with LTO-6, the compression ratio became 2.5:1.
With the WORM feature added in LTO-3, an organization cannot overwrite data, ensuring a level of safety for its data storage. WORM also helps with compliance regulations and reduces the risk of data loss caused by human error.
Encryption, added in LTO-4, enhances security and privacy. The 256-bit Advanced Encryption Standard with the Galois/Counter Mode algorithm happens at the LTO-drive level, which provides compression before encryption, thus maximizing tape capacity. As tapes are often transported, encryption is important to keep data secure.
LTFS partitioning, added in LTO-5, improves file control and space management. Through indexing, the feature tells the drive where a file is stored on the tape. The drive reads the indexing information, which is then presented in a format that enables the user to drag and drop files, similar to using a thumb drive, according to the LTO Program.
As LTO is still a serial recording device, the user can only access data at the end of a tape cartridge by running through its full length. The user must download software for an OS to recognize LTFS.
Benefits/drawbacks of magnetic tape
Tape capacity continues to grow at a consistent rate. A reliable product roadmap is a plus for LTO users, as they know a new edition will come out every two to three years and will likely double the previous edition's capacity.
Storing 30 TB of compressed data on an LTO-8 tape is generally less expensive than using flash or hard disk for that type of storage. LTO tape also does not require electricity for storage and can last up to 30 years. In addition, LTO-7 and LTO-8 tapes have a bit error rate of 1 x 10-19, which the LTO Program says is four times better than disk.
Barium ferrite on LTO cartridges has demonstrated the potential of providing uncompressed capacities per tape cartridge of up to 220 TB. Even with large capacities, LTO is portable.
The 12 TB of uncompressed capacity in LTO-8 can hold up to 7,140,000 photos; 2,880,000 songs; or 8,000 movies, according to tape library and media vendor Spectra Logic. With businesses frequently storing terabytes or petabytes of data, capacity is an important part of storage.
The open tape format makes for a more competitive environment, leading to innovation and enhancements. LTO products, though, are not compatible with non-LTO products.
Tape has linear access. In addition to providing faster restore speeds, a hard disk offers random access. As a result, a disk may be better for backup than magnetic tape.
However, when an organization accesses certain data less frequently, it should move that data to tape, according to the LTO Consortium. For example, archived data, which is commonly kept for compliance and regulatory reasons, is not usually needed right away and can find a good home on tape.
The cloud has become popular for backup. It is easily scalable and provides random access. Cloud storage can be cheaper than tape, especially for SMBs that don't create the volumes of data that enterprises using tape can produce. Restoring data from the cloud, though, is often slow, especially if it is a large volume of data or there is weak bandwidth.
Digital linear tape (DLT) is another type of magnetic tape used for storage and archiving. Digital Equipment Corp. developed the DLT technology in the 1980s. In 1994, Quantum purchased the technology. Quantum has since adopted the LTO standard. DLT tapes are still available from Quantum and other manufacturers.
Major vendors
On its website, the LTO Program lists manufacturers that have passed compliance verification requirements to sell LTO Ultrium-branded tape drives and cartridges. As of June 2018, they include:
- Fujifilm
- HPE
- IBM
- Imation (now Glassbridge Enterprises)
- Maxell
- NXP Semiconductors
- Quantum
- Sony
- Spectra Logic
- Teijin DuPont Films
LTO trends and future direction
As of June 2018, the LTO roadmap has been projected to the 12th generation. All future generations on the roadmap are expected to feature WORM, encryption and LTFS.
LTO-9: Expected to provide 24 TB of uncompressed capacity and 60 TB compressed. As of June 2018, the LTO Consortium had not announced a launch date for LTO-9, nor the expected data transfer rates.
LTO-10: Expected to provide 48 TB of uncompressed capacity and 120 TB compressed.
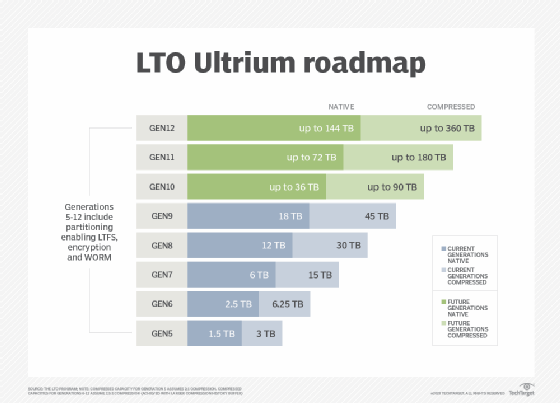
LTO-11: Expected to provide 96 TB of uncompressed capacity and 240 TB compressed.
LTO-12: Expected to provide 192 TB of uncompressed capacity and 480 TB compressed.
Because each new version provides a large capacity increase, and with LTO drives now only able to read back one generation, users will be more likely to upgrade to a newer LTO tape format right away.
There is still a lot of room to grow LTO cartridge capacity. In August 2017, IBM and Sony announced they have developed technology that can support about 330 TB of uncompressed storage per tape cartridge.






